About the Project
SRS Simple Hits Counter is a simple plugin to count and show the total number hits (Unique visitors and page views) to the site without using any third party code.
As the name suggests, it’s a very simple Hit Counter that counts the number of Unique Visitors and Page-views. You can show either the unique visitors or total page views count anywhere on the site using WordPress widgets or the WordPress shortcode. You can also add/show both hit counters(Visitors and Page views) by using two copies of the WordPress widget or the WordPress shortcode. It keeps counting even when you have no WordPress widget or WordPress shortcode active so it can be used as an analytics tool as well. To completely disable the counter you have to deactivate the plugin.
Features
- AJAX based counter ignores most bots or crawlers
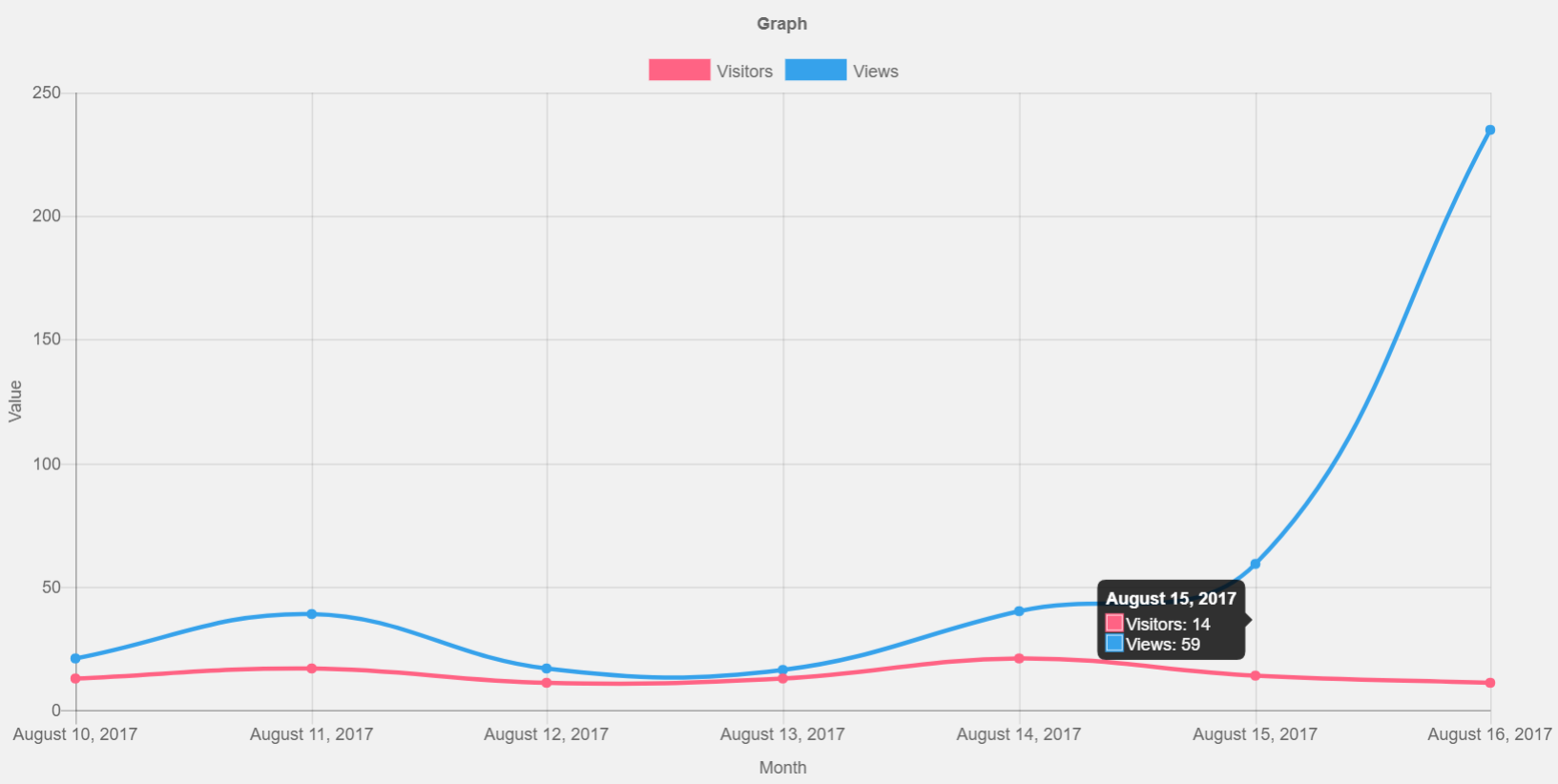
- Monthly and weekly graph
- Show Unique visitors and Page views
- Ability to reset the counter to any number
- Show anywhere on the site using WordPress widgets and WordPress shortcode
Shortcodes
- Unique visitors = srs_total_visitors
- Page views = srs_total_pageViews
Installation
From your WordPress dashboard
1. Visit ‘Plugins > Add New’
2. Search for ‘SRS Simple Hits Counter’
3. Activate ‘SRS Simple Hits Counter’ from your Plugins page.
4. Use widget to display the counter in footer or sidebar etc.
5. Use the shortcode to add the counter to any part of the site.
From WordPress.org
1. Download ‘SRS Simple Hits Counter’.
2. Upload the ‘SRS Simple Hits Counter’ directory to your ‘/wp-content/plugins/’ directory, using your favorite method (ftp, sftp, scp, etc…)
3. Activate ‘SRS Simple Hits Counter’ from your Plugins page.
4. Use widget to display the counter in footer or sidebar etc.
5. Use the shortcode to add the counter to any part of the site.
Demo
Unique Visitors
365,240
Page-views
668,690